Concluding Remarks¶
In this lecture, ‘Introduction to Machine Learning for the Sciences’, we have discussed common structures and algorithms of machine learning to analyze data or learn policies to achieve a given goal. Even though machine learning is often associated with neural networks, we have first introduced methods commonly known from statistical analysis, such as linear regression. Neural networks, which we used for most of this lecture, are much less controlled than these conventional methods. As an example, we do not try to find an absolute minimum in the optimization procedure, but one of many almost degenerate minima. This uncertainty might feel like a loss of control to a scientist, but it is crucial for the successful generalization of the trained network
The goal of our discussions was not to provide the details needed for an actual implementation—as all standard algorithms are provided by standard libraries such as TensorFlow or PyTorch, this is indeed not necessary—but to give an overview over the most important terminology and the common algorithms. We hope that such an overview is helpful for reading the literature and deciding, whether a given method is suitable for your own problems.
To help with the use of machine learning in your own research, here a few lessons for a successful machine learner:
Your learning result can only be as good as your data set.
Understand your data, its structure and biases.
Try simpler algorithms first.
Don’t be afraid of lingo. Not everything that sounds fancy actually is.
Neural networks are better at interpolating than extrapolating.
Neural networks represent smooth functions well, not discontinuous or spiky ones.
Regarding the use of machine learning in a scientific setting, several points should be kept in mind. First, unlike in many other applications, scientific data often exhibits specific structure, correlations, or biases, which are known beforehand. It is thus important to use our prior knowledge in the construction of the neural network and the loss function. There are also many situations, where the output of the network has to satisfy conditions, such as symmetries, to be meaningful in a given context. This should ideally be included in the definition of the network. Finally, scientific analysis needs to be well defined and reproducible. Machine learning, with its intrinsic stochastic nature, does not easily satisfy these conditions. It is thus crucial to document carefully the architecture and all hyperparameters of a network and training. The results should be compared to conventional statistical methods, their robustness to variations in the structure of the network and the hyperparameters should be checked.
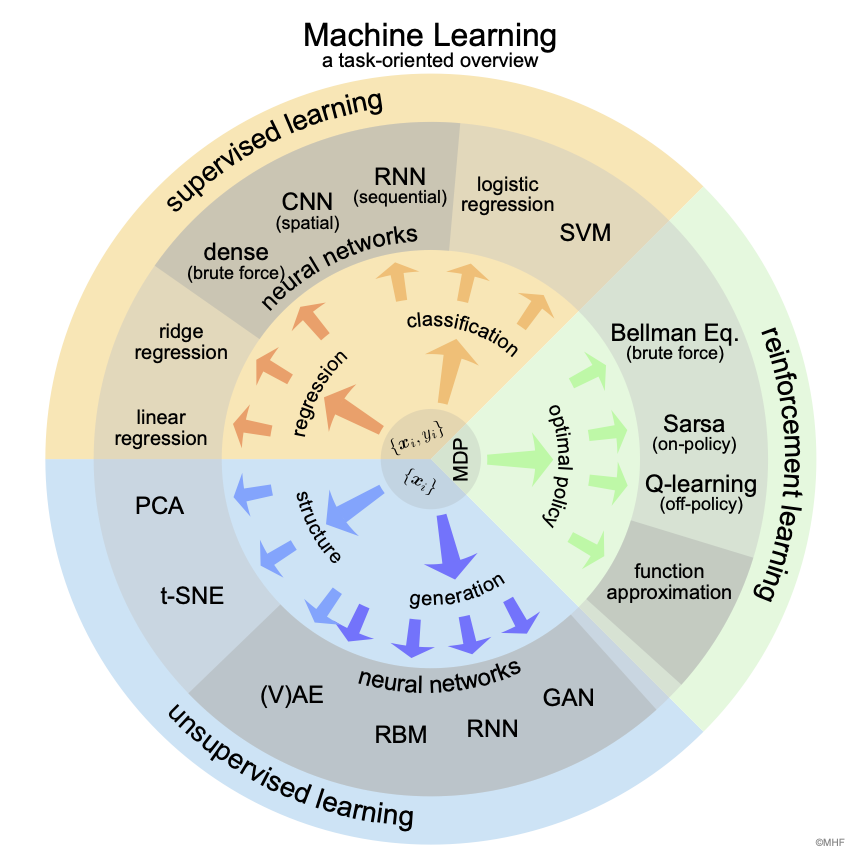
Fig. 36 Machine Learning overview. Methods covered in this lecture from the point of view of tasks.¶